四舵轮底盘运动解算
舵轮具备向任意方向产生速度的能力,因此舵轮底盘可以进行全向运动。
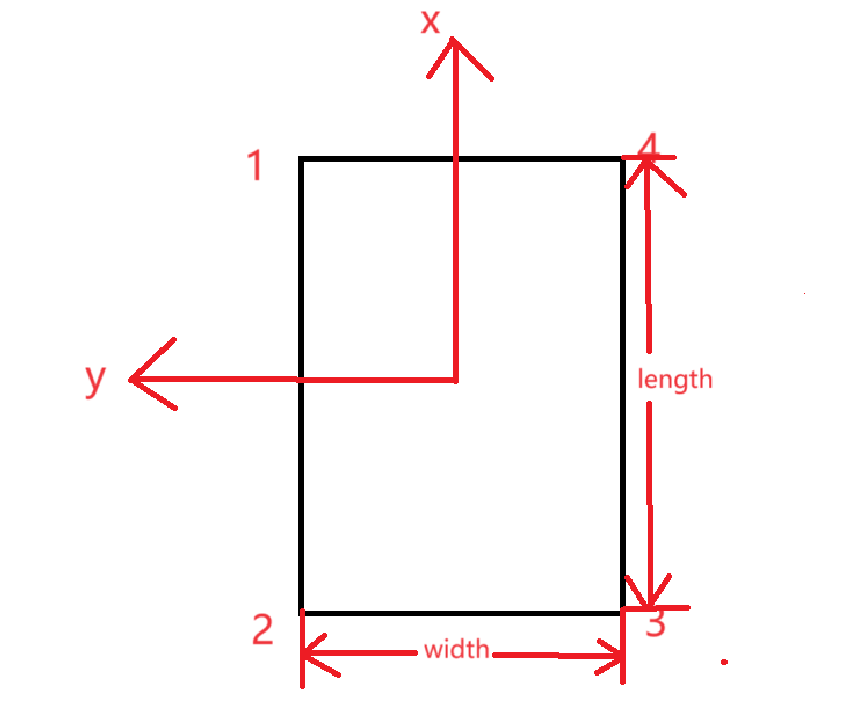
定义底盘坐标系如下,x为正前方,原点为底盘中心。
底盘的运动状态可以表示为 \[ \boldsymbol{V}=\begin{bmatrix} \vec{v}& \vec{\omega}\end{bmatrix} \] 其中\(v\)表示底盘在\(X-Y\)平面的线速度,\(\omega\)表示底盘绕自身中心自转的角速度。
令\(\theta=\arctan(\frac{l}{w})\),\(\vec{r_i}\)为车体中心指向轮子中心的向量,\(|\vec{r_i}|=\frac{\sqrt{l^2+w^2}}{2}\)
我们将角速度\(\omega\)映射到四个轮子上,于是有 \[ \vec{v_{\omega i}}=\vec{\omega}\times \vec{r_i}=|\vec\omega||\vec{r_i}|(\cos(\theta_i),sin(\theta_i)) \] 其中 \[ \begin{bmatrix} \theta_1\\ \theta_2\\ \theta_3\\ \theta_4 \end{bmatrix}= \begin{bmatrix} \pi-\theta\\ \theta-\pi\\ -\theta\\ \theta \end{bmatrix} \]
将线速度\(v\)映射到四个轮子上,于是有 \[ \vec{v_{li}}=\vec{v}=\begin{bmatrix}v_x\\v_y\end{bmatrix} \] 把线速度的投影和角速度的投影相加,得到 \[ \vec{v_{i}}=\vec{v_{li}}+\vec{v_{\omega i}} \] 于是我们有 \[ \vec{v_i}=\begin{bmatrix} 1 & 0 & |r|\cos(\theta_i)\\ 0 & 1 & |r|\sin(\theta_i) \end{bmatrix} \begin{bmatrix} v_x\\ v_y\\ \omega \end{bmatrix} \]
将所得的矢量的模作为舵轮的速度,矢量的方向作为舵轮的方向即可。